Suppose
T is a
binary tree
Then T is
called binary search tree if each node N of
T
has the following property
The
value at N is greater
than every value in the left sub-tree of N and is less than
every value in the right sub-tree of N
Binary Search Tree (BST)
Two binary search trees representing the same set:
Average
depth of a node is O(log N); maximum depth of a node is O(N)
Searching and Inserting in BST
Algorithm
to find the location of ITEM
in the BST T
or
insert ITEM
as
a new node in its appropriate place in the tree
[a]
Compare ITEM with the root node N of the
tree
(i)
If ITEM < N, proceed to the left child of N
(ii)
If ITEM > N, proceed to the right child of N
[b]
Repeat Step (a) until one of the following occurs
(i)
We meet a node N such that ITEM = N. In this case search is successful
(ii)
We meet an empty sub-tree, which indicates that search is unsuccessful and we
insert ITEM in place of empty subtree
Searching BST
•If we are searching for 15, then we
are done.
•If we are searching for a key <
15, then we should search in the left subtree.
•If we are searching for a key >
15, then we should search in the right subtree.
Example :
Example demo :
Insert 40, 60, 50, 33, 55, 11 into an empty BST
Insert
40, 60, 50, 33, 55, 11 into an empty BST
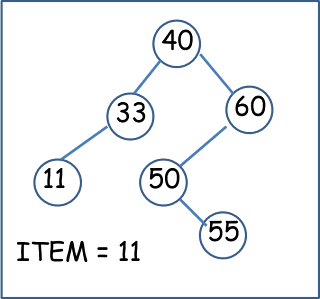
Locating an ITEM
A binary search tree T is in memory
and an ITEM of information is given. This procedure finds the location LOC of
ITEM in T and also the location of the parent PAR of ITEM
Three
special cases:
[1]
LOC == NULL and PAR == NULL, tree is empty
[2]
LOC ¹
and PAR == NULL, ITEM is the root of T
ALGORIthm :
[1]
[Tree empty ?]
If ROOT == NULL, then
Set LOC = NULL, PAR = NULL, Exit
[2]
[ITEM at root ?]
If ROOT->INFO == ITEM, then
Set LOC = ROOT, PAR = NULL, Exit
[3]
[Initialize pointer PTR and SAVE]
If ITEM < ROOT->INFO then
Set PTR = ROOT->LEFT, SAVE = ROOT
Else
Set PTR = ROOT->RIGHT, SAVE =ROOT
[4]
Repeat Step 5 and 6 while PTR ¹
NULL
[5]
[ITEM Found ?]
If ITEM == PTR->INFO, then
Set LOC = PTR, PAR = SAVE, Exit
[6] If ITEM < PTR->INFO, then
Set SAVE = PTR, PTR = PTR->LEFT
Else
Set SAVE = PTR, PTR = PTR->RIGHT
[7]
[Search Unsuccessful]
Set LOC = NULL, PAR = SAVE
[8]
Exit
A
binary search Tree T is in memory and an ITEM of information is given.
Algorithm to find the location LOC of ITEM in T or adds ITEM as a new node in T
at location LOC.
[1]
Call FIND(INFO, LEFT,RIGHT,ROOT,ITEM,LOC,PAR)
[2]
If LOC ¹
NULL, then Exit
[3]
[Copy the ITEM into the node NEW]
(a) Create a node NEW
(b) NEW->INFO = ITEM
( c) Set LOC = NEW, NEW->LEFT = NULL,
NEW->RIGHT = NULL
[4]
[Add ITEM to tree]
If PAR = NULL
Set ROOT = NEW
Else
If ITEM < PAR->INFO, then
Set PAR->LEFT = NEW
Else
Set PAR->RIGHT = NEW
[5]
Exit
Insert Algorithm
• If value we want to insert < key
of current node, we have to go to the left subtree
• Otherwise we have to go to the
right subtree
•If the current node is empty (not
existing) create a node with the value we are inserting and place it here.
For
example, inserting ’15’ into the BST?
Deletion from BST
T is
a binary tree. Delete an ITEM from the tree T
Deleting
a node N
from tree depends primarily on the number of children of node N
There
are three cases in deletion
Case
1.
N has no children. N is deleted from the T by replacing the location of N
in the parent node of N by null pointer
Case
2.
N has exactly one children. N is deleted from the T by simply replacing the
location of N in the parent node of N by
the location of the only child of N
Case
3.
N has two children. Let S(N) denote the
in-order successor of N. Then N is
deleted from the T by first deleting S(N) from T and then replacing node
N in T by the node S(N)
Types of Binary Trees
•Degenerate – only one child
•Balanced – mostly two children
•Complete – always two children
Binary Trees Properties
–Degenerate
•Height = O(n) for n nodes
•Similar to linear list
-Balanced
–Height = O( log(n) ) for n nodes
–Useful for searches
•Key property Of BST
–Value at node
•Smaller values in left subtree
•Larger values in right subtree
–Example
•X > Y
•X < Z
Binary Search Properties
•Time of search
–Proportional to height of tree
–Balanced binary tree
•O( log(n) ) time
–Degenerate tree
•O( n ) time
•Like searching linked list /
unsorted array
•Requires
–Ability to compare
key values
Binary Search Tree Construction
•How to build & maintain binary
trees?
–Insertion
–Deletion
•Maintain key property (invariant)
–Smaller values in left subtree
–Larger values in right subtree
Binary Search Tree – Insertion
•Algorithm
Perform
search for value X
Search
will end at node Y (if X not in tree)
If X
< Y, insert new leaf X as new left subtree
for Y
If X
> Y, insert new leaf X as new right subtree
for Y
•Observations
–O( log(n) ) operation for balanced
tree
–Insertions may unbalance tree
No comments:
Post a Comment
THANKS FOR UR GREAT COMMENT